algoritmo de Kruskal
árbol de coste total mínimo/máximo
Joseph B. Kruskal investigador del Math Center (Bell-Labs), que en 1956 descubrió su algoritmo para la resolución del problema del Árbol de coste total mínimo (minimum spanning tree - MST) también llamado árbol recubridor euclídeo mínimo. Este problema es un problema típico de optimización combinatoria, que fue considerado originalmente por Otakar Boruvka (1926) mientras estudiaba la necesidad de electrificación rural en el sur de Moravia en Checoslovaquia.
El objetivo del algoritmo de Kruskal es construir un árbol (subgrafo sin ciclos) formado por arcos sucesivamente seleccionados de mínimo peso a partir de un grafo con pesos en los arcos.
Un árbol (spanning tree) de un grafo es un subgrafo que contiene todos sus vértices o nodos. Un grafo puede tener múltiples árboles. Por ejemplo, un grafo completo de cuatro nodos (todos relacionados con todos) tendría 16 árboles.
La aplicación típica de este problema es el diseño de redes telefónicas. Una empresa con diferentes oficinas, trata de trazar líneas de teléfono para conectarlas unas con otras. La compañía telefónica le ofrece esta interconexión, pero ofrece tarifas diferentes o costes por conectar cada par de oficinas. Cómo conectar entonces las oficinas al mínimo coste total.
La formulación del MST también ha sido aplicada para hallar soluciones en diversas áreas (diseño de redes de transporte, diseño de redes de telecomunicaciones - TV por cable, sistemas distribuidos, interpretación de datos climatológicos, visión artificial - análisis de imágenes - extracción de rasgos de parentesco, análisis de clusters y búsqueda de superestructuras de quasar, plegamiento de proteínas, reconocimiento de células cancerosas, y otros).
Otra aplicación menos obvia es que el árbol de coste total mínimo puede ser usado como solución aproximada al problema del viajante de comercio (traveling salesman problem), recuerde que encontrar la solución óptima a este problema es NP-Hard. La manera formal de definir este problema es encontrar la trayectoria más corta para visitar cada punto al menos una vez. Nótese que si se visitan todos los puntos exactamente una vez, lo que se tiene es un tipo especial de árbol. En el ejemplo anterior, 12 de los 16 árboles son trayectorias de este tipo. Si se tiene una trayectoria que visita algunos vértices o nodos más de una vez, siempre se puede soltar algunos nodos del árbol. En general el peso del árbol total mínimo es menor que el del viajante de comercio, debido a que su minimización se realiza sobre un conjunto estrictamente mayor. Existen diferentes algoritmos y maneras de usar el árbol de coste total mínimo para encontrar la solución al problema del viajante de comercio (con resultados cercanos al óptimo).
algoritmo de Kruskal (árbol de coste total mínimo)
Dado un grafo G con nodos conectados por arcos con peso (coste o longitud): el peso o coste total de un árbol será la suma de pesos de sus arcos. Obviamente, árboles diferentes tendrán un coste diferente. El problema es entonces ¿cómo encontrar el árbol de coste total mínimo?
Una manera de encontrar la solución al problema del árbol de coste total mínimo, es la enumeración completa. Aunque esta forma de resolución es eficaz, no se puede considerar un algoritmo, y además no es nada eficiente.
Este problema fue resuelto independientemente por Dijkstra (1959), Kruskal (1956) y Prim (1957) y la existencia de un algoritmo polinomial (que todos ellos demostraron) es una grata sorpresa, debido a que un grafo con N vértices puede llegar a contener N^N-2 subárboles. A lo largo de la historia se ha hecho un gran esfuerzo para encontrar un algoritmo rápido para este problema. El algoritmo de Kruskal es uno de los más fáciles de entender y probablemente el mejor para resolver problemas a mano.
El algoritmo se basa en una propiedad clave de los árboles que permite estar seguros de si un arco debe pertenecer al árbol o no, y usar esta propiedad para seleccionar cada arco. Nótese en el algoritmo, que siempre que se añade un arco (u,v), éste será siempre la conexión más corta (menor coste) alcanzable desde el nodo u al resto del grafo G. Así que por definición éste deberá ser parte del árbol.
Este algoritmo es de tipo greedy, ya que a cada paso, éste selecciona el arco más barato y lo añade al subgrafo. Este tipo de algoritmos pueden no funcionar para resolver otro tipo de problemas, por ejemplo para encontrar la ruta más corta entre los nodos a y b.
Para simplificar, se asumirán que existe un único árbol de coste total mínimo, aunque en muchos problemas puede existir más de una solución optima de igual valor total mínimo.
A continuación se muestra el pseudocódigo del algoritmo:
Kruskal (G)
E(1)=0, E(2)= todos los Arcos del grafo G
Mientras E(1) contenga menos de n-1 arcos y E(2)=0 do
De los arcos de E(2) seleccionar el de menor coste -->e(ij)
E(2)= E(2) - {e(ij)}
Si V(i), V(j) no están en el mismo árbol entonces
juntar los árboles de V(i) y de V(j) en uno sólo
end Si
end do
Fin del algoritmo
Este problema puede ser resuelto por diferentes algoritmos, e incluso en la actualidad sigue siendo tema de interés en investigaciones. Es interesante la lectura de los siguientes algoritmos (que resuelven este problema para diferentes supuestos), aunque son bastante complejos y probablemente no requiera utilizarlos a no ser que trabaje con grafos de grandes dimensiones:
- Karger, Klein, and Tarjan, A randomized linear-time algorithm to find minimum spanning trees, J. ACM, vol. 42, 1995, pp. 321-328.
- Fredman and Willard, Trans-dichotomous algorithms for minimum spanning trees and shortest paths, 31st IEEE Symp. Foundations of Comp. Sci., 1990, pp. 719-725.
- Gabow, Galil, Spencer, and Tarjan, Efficient algorithms for finding minimum spanning trees in undirected and directed graphs. Combinatorica, vol. 6, 1986, pp. 109-122.
Puede encontrar más información en:
- J. B. Kruskal. On the shortest spanning subtree of a graph and the traveling salesman problem. Proc. of the American Mathematical Society, 7:48-50, 1956.
ejemplo de árbol de coste total mínimo
Construya un grafo a partir de la siguiente matriz de datos:
N1\N2 a b c d e f g h i a 4 8 b 8 11 c 8 7 4 2 d 7 9 14 e 9 10 f 4 14 10 2 g 2 6 1 h 2 6 7 i 8 11 1 7
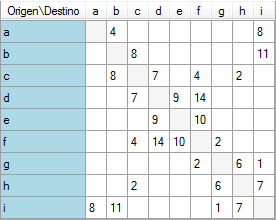El grafo dibujado tendrá el siguiente aspecto.
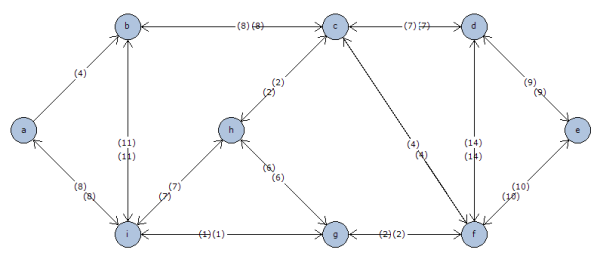
No se requiere de la selección de ningún nodo para la ejecución del algoritmo, la representación del resultado será la siguiente.
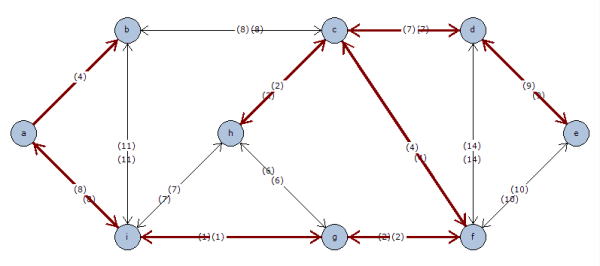
Donde se muestra que el árbol de coste mínimo para este ejemplo tiene un coste total de 37 unidades.
* a ----(4)---> b * d ----(7)---> c * e ----(9)---> d * f ----(4)---> c * g ----(2)---> f * h ----(2)---> c * i ----(8)---> a * i ----(1)---> g Coste total = 37 Matriz de Arcos del árbol con coste mínimo: N1\N2 a b c d e f g h i a 0 1 0 0 0 0 0 0 0 b 0 0 0 0 0 0 0 0 0 c 0 0 0 0 0 0 0 0 0 d 0 0 1 0 0 0 0 0 0 e 0 0 0 1 0 0 0 0 0 f 0 0 1 0 0 0 0 0 0 g 0 0 0 0 0 1 0 0 0 h 0 0 1 0 0 0 0 0 0 i 1 0 0 0 0 0 1 0 0
árbol de coste máximo
Del mismo modo se puede calcular el árbol de coste máximo, que en este ejemplo tendrá un coste total de 71 unidades, tal y como muestran la siguiente figura y la tabla de resultados.
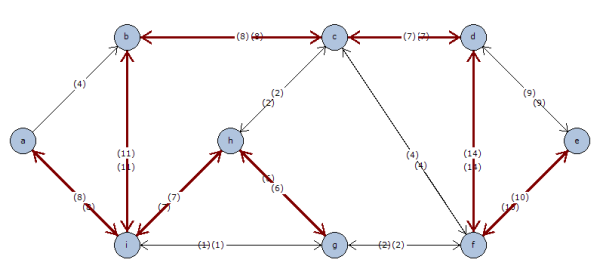
* c ----(8)---> b * d ----(7)---> c * f ----(14)---> d * f ----(10)---> e * h ----(6)---> g * i ----(8)---> a * i ----(11)---> b * i ----(7)---> h Coste total = 71 Matriz de Arcos del árbol con coste máximo: N1\N2 a b c d e f g h i a 0 0 0 0 0 0 0 0 0 b 0 0 0 0 0 0 0 0 0 c 0 1 0 0 0 0 0 0 0 d 0 0 1 0 0 0 0 0 0 e 0 0 0 0 0 0 0 0 0 f 0 0 0 1 1 0 0 0 0 g 0 0 0 0 0 0 0 0 0 h 0 0 0 0 0 0 1 0 0 i 1 1 0 0 0 0 0 1 0