algoritmo de Ford-Fulkerson
flujo máximo


Lester Randolph Ford Jr. al continuar los pasos de su padre Ford Sr. también hizo una enorme contribución al campo de las matemáticas. Su trabajo con Delbert Ray Fulkerson (14 agosto de 1924 - 10 Enero de 1976) ha puesto la base de casi toda la investigación en flujos de grafos. El artículo de Ford y de Fulkerson (1956) con el problema de flujo máximo estableció el famoso teorema del flujo máximo - mínimo corte.
Se puede considerar un grafo como una red de flujo. Donde un nodo fuente produce o introduce en la red cierta cantidad de algún tipo de material, y un nodo sumidero lo consume. Cada arco, por tanto, puede considerarse como un conducto que tiene cierta capacidad de flujo. De igual modo que en redes eléctricas (Leyes de Kirchhoff), la suma de flujos entrantes a un nodo, debe ser igual a la suma de los salientes (principio de conservación de energía), excepto para el nodo fuente y el nodo sumidero.
Por tanto, el problema de flujo máximo se enuncia como: ¿cuál es la tasa a la cual se puede transportar el material desde el nodo fuente al nodo sumidero, sin violar las restricciones de capacidad?. Este algoritmo se puede usar para resolver modelos de: transporte de mercancías (logística de aprovisionamiento y distribución), flujo de gases y líquidos por tuberías, componentes o piezas en líneas de montaje, corriente en redes eléctricas, paquetes de información en redes de comunicaciones, tráfico ferroviario, sistema de regadíos, etc.
Una red de flujo es un grafo dirigido G=(V,E) donde cada arco (u,v) perteneciente a E el número de arcos del grafo; tiene una capacidad no negativa. Se distinguen dos nodos: la fuente o nodo s, y el sumidero o nodo t. Si existen múltiples fuentes y sumideros, el problema se puede simplificar añadiendo una fuente común y un sumidero común. Este algoritmo depende de tres conceptos principales:
- Un camino de aumento, es una trayectoria desde el nodo fuente s al nodo sumidero t que puede conducir más flujo.
- La capacidad residual es la capacidad adicional de flujo que un arco puede llevar c_f (u,v) = c(u,v) - f(u,v)
- Teorema de Ford-Fulkerson (1962): En cualquier red, el flujo máximo que fluye de la fuente al destino es igual a la capacidad del corte mínimo que separa a la fuente del destino.
El algoritmo es iterativo, se comienza con f(u,v)=0 para cada par de nodos y en cada iteración se incrementa el valor del flujo buscando un camino de aumento. El proceso se repite hasta no encontrar un camino de aumento. A continuación se muestra el pseudocódigo del algoritmo:
Ford-Fulkerson (G,s,t)
para cada arco (u,v) de E
f(u,v) = 0
f(v,u) = 0
mientras exista un camino p desde s a t en la red residual G_f
c_f (p) = min {c_f (u,v) : (u,v) está sobre p}
para cada arco (u,v) en p
f(u,v) = f(u,v) + c_f (p)
f(u,v) = -f(u,v)
Una variación del algoritmo de Ford-Fulkerson es el algoritmo de Edmonds-Karp (J. Edmonds; R.M. Karp - 1972). En éste, el 'camino de aumento' es elegido usando una búsqueda por niveles o en anchura (breadth-first search). El algoritmo de Edmonds-Karp requiere O(VE^2) tiempo de computación, donde V es el número de nodos o vértices, y E el número de arcos del grafo.
Puede encontrar más información en:
- Ford, L. R. and Fulkerson, D. R. Flows in Networks. Princeton, NJ. Princeton University Press, 1962.
- Edmonds, J. and Karp, R. M. Theoretical Improvements in Algorithmic Efficiency for Network Flow Problems. J. ACM 19, 248-264, 1972.
- Berge, C. Two Theorems in Graph Theory. Proc. Nat. Acad. Sci. USA 43, 842-844, 1957.
ejemplo de flujo máximo
Para el presente ejemplo, construiremos una grafo con las siguientes matrices de datos para los valores mínimo, máximo y coste de los arcos:
Matriz de mínimo: N1\N2 s 1 2 3 4 t s 12 11 1 12 0 2 0 19 3 0 11 4 7 4 t Matriz de máximo: N1\N2 s 1 2 3 4 t s 16 13 1 12 10 2 9 20 3 4 14 4 7 4 t Matriz de coste: N1\N2 s 1 2 3 4 t s 0 0 1 0 0 2 0 0 3 0 0 4 0 0 t
El grafo dibujado tendría el siguiente aspecto.
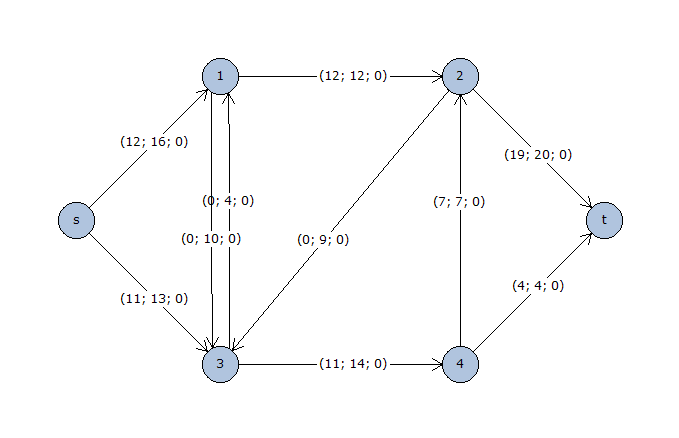
Nótese que en los arcos se han representado los valores de mínimo, máximo y coste respectivamente. Antes de iniciar el algoritmo se deben seleccionar un nodo origen y un nodo destino, en este ejemplo se tomará el nodo s y el nodo t respectivamente.
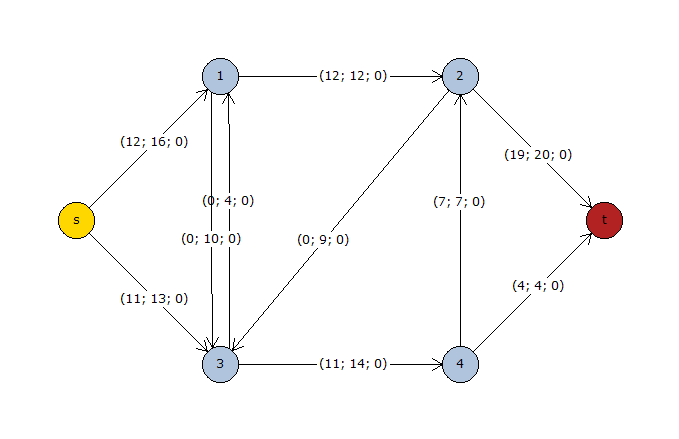
Tras ejecutar el algoritmo se muestra la siguiente solución:
Flujos calculados desde el nodo origen (s) hasta el nodo destino (t) Flujo máximo = 23 Matriz de Arcos con flujo máximo: N1\N2 s 1 2 3 4 t s 0 12 0 11 0 0 1 -12 0 12 0 0 0 2 0 -12 0 0 -7 19 3 -11 0 0 0 11 0 4 0 0 7 -11 0 4 t 0 0 -19 0 -4 0 Matriz de Capacidades Residuales: N1\N2 s 1 2 3 4 t s 0 4 0 2 0 0 1 12 0 0 10 0 0 2 0 12 0 9 7 1 3 11 4 0 0 3 0 4 0 0 0 11 0 0 t 0 0 19 0 4 0
Como se puede observar, el flujo máximo es de 23 unidades. A continuación Grafos subrayará los arcos de la solución, diferenciando el color ligeramente para distinguir los arcos saturados de aquellos que tienen capacidad residual.
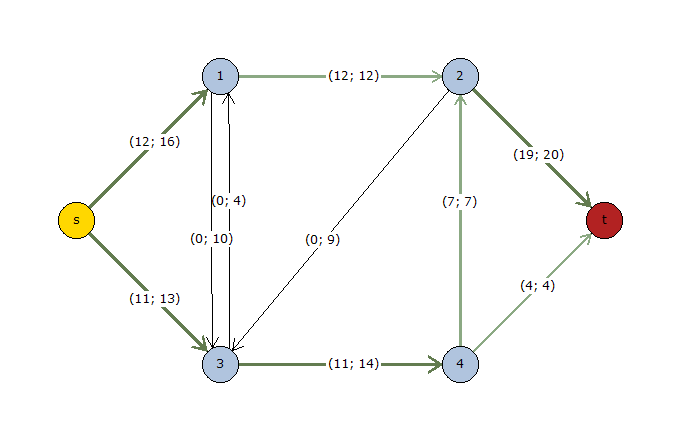
Si observa la figura verá cómo todo el flujo originario del nodo s se distribuye por los arcos de la red, hasta llegar al nodo destino t. Nótese además, que en este algoritmo no se han tenido en cuenta los costes asociados al transporte o flujo, simplemente las conexiones y la restricción/capacidad de flujo de los arcos.