algoritmo de Bellman-Ford
camino mínimo - camino máximo
Lester Randolph Ford Jr. es uno de los pioneros en el campo de la programación de flujos en grafos. Es el hijo de L.R. Ford Sr. (quién también es un matemático distinguido) y nació el 23 de septiembre de 1927. L. R. Ford Sr es elogiado por su ejemplar trabajo en matemáticas al inventar una interpretación geométrica absolutamente maravillosa de la serie de Farey. También le acredita su trabajo 'Pointwise Discontinuous Functions' que era la base de su trabajo para un grado de M.S. del departamento de matemáticas en la universidad de Missouri-Colombia en 1912. Tal fue su contribución a las matemáticas, que en 1964 se estableció el Lester R. Ford Award para reconocer la contribución a las matemáticas de excelentes autores matemáticos publicados en The American Mathematical Monthly o Mathematics Magazine. Fue redactor de American Mathematical Monthly, de 1942-1946, y el presidente de Mathematical Association of America, 1947-1948. Ford Sr. y Ford Jr. son co-autores de Automorphic Functions cuál fue publicado cerca por McGraw-Hill en 1963.
Mientras trabajó en RAND CORPORATION, Ford Jr publicó numerosos artículos que no solo establecieron la base de los flujos de red sino también la futura investigación en este campo. En 1962 Priceton University Press publicó su libro Flow in Networks con D. R. Fulkerson como co-autor. Este libro contiene todo su trabajo sobre redes.
Junto con Richard E. Bellman 
(26 de agosto 1920 – 19 marzo de 1984) desarrollaron el algoritmo de 'corrección de etiquetas' que calcula el camino más corto en un digrafo ponderado (donde incluso y a diferencia de Dijkstra, los pesos de los arcos pueden ser negativos).
La mayoría del trabajo de Ford lo hizo en la colaboración con Fulkerson, al parecer los dos hacían una buena asociación. Sin embargo, en 1956 presentó varios artículos firmados por él sólo. Ha sido el autor de diversos algoritmos que se han refinado con los años y que todavía se utilizan para solucionar la mayoría de problemas de grafos.
algoritmo de Bellman-Ford (camino mínimo)
Soluciona el problema de la ruta más corta o camino mínimo desde un nodo origen, de un modo más general que el Algoritmo de Dijkstra, ya que permite valores negativos en los arcos.
El algoritmo devuelve un valor booleano si encuentra un circuito o lazo de peso negativo. En caso contrario calcula y devuelve el camino mínimo con su coste. Para cada vértice v perteneciente a V, se mantiene el atributo d[v] como cota superior o coste del camino mínimo desde el origen s al vértice v. A continuación se muestra el pseudocódigo del algoritmo:
Bellman-Ford (G,s)
Inicializar
for cada v perteneciente a V[G]
do d[v] = infinito
p[v] = nulo
p[s] = 0
for i=1 to V[G]-1
do for cada arco (u,v) perteneciente a A[G]
Relajación
if d[v] > d[u] + w(u,v) then
d[v] = d[u] + w(u,v)
p(v) = u
for cada arco (u,v) chequea lazo de peso negativo
do if d[v] > d[u] + w(u,v) then
return FALSO 'el algoritmo no converge
return VERDADERO
algoritmo de Bellman-Ford (camino máximo)
El problema de la ruta más larga puede ser transformado en el de ruta más corta cambiando el signo de los costes de los arcos. De manera alternativa se puede transformar también cambiando los procesos de inicialización y relajación. En este caso el problema es inconsistente para circuitos de peso positivo.
Inicializar
for cada v perteneciente a V[G]
do d[v] = - infinito
p[v] = nulo
p[s] = 0
Relajación
if d[v] < d[u] + w(u,v) then
d[v] = d[u] + w(u,v)
p(v) = u
Puede encontrar más información en:
- Bellman, R. E., On a routing problem, quarterly of Applied Mathematics, 16, 87-90, 1958.
- Ford, L. R.Jr., Network Flow Theory, Paper P-923, RAND Corporation, Santa Monica, California, 1956.
ejemplo de camino mínimo
El proceso de utilización y la interpretación de los resultados es exactamente la misma que en el caso del algoritmo de Dijkstra. Tras construir el grafo, se de seleccionar un nodo origen y un nodo destino antes de ejecutar el algoritmo. Los resultados deberían ser los mismos que en el caso del algoritmo de Dijkstra, pero puede ocurrir que el grafo tenga varias soluciones óptimas y que cada uno de estos algoritmos muestre una de ellas.
En el ejemplo sencillo utilizado anteriormente, ambas soluciones coinciden en el mismo camino de mínimo coste 7 unidades.
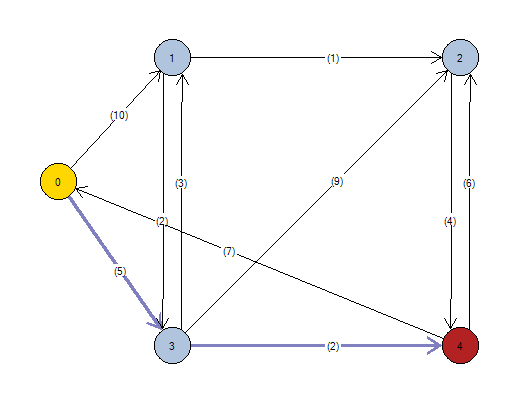
Arcos calculados desde el nodo origen (0) hasta el nodo destino (4): * 0 ----(5)---> 3 * 3 ----(2)---> 4 Coste total = 7 Matriz de Arcos con coste mínimo: N1\N2 0 1 2 3 4 0 0 0 0 1 0 1 0 0 0 0 0 2 0 0 0 0 0 3 0 0 0 0 1 4 0 0 0 0 0