problema de transbordo / transporte
a coste mínimo
En este apartado se comentará la aplicación de la teoría de grafos para la resolución y optimización del flujo en una red. Concretamente se hablará de los problemas de suministro y demanda.
Dado un grafo <tex>G</tex> con vértices o nodos <tex>V</tex> conectados entre sí y clasificados en dos conjuntos <tex>X</tex> e <tex>Y</tex>. Los nodos <tex>x</tex> se considerarán como elementos de suministro (por ejemplo plantas productivas o proveedores), mientras que los nodos <tex>y</tex> se entenderán como elementos de demanda (clientes cuya demanda hay que satisfacer). El objetivo será encontrar el flujo (transporte de mercancías a través de la red) con origen en los nodos <tex>x</tex> y destino en los <tex>y</tex>, que satisfaga una serie de restricciones que dependerán del problema particular a resolver.
En la literatura, existen multitud de heurísticas y algoritmos optimizadores para resolver algunos de estos casos particulares (por ejemplo una versión especial del algoritmo Simplex para Programación Lineal llamado Network Simplex Algorithm). Asimismo, también existen generalizaciones del problema (multiterminal), o incluso variantes con perdida de flujo en los arcos (por ejemplo la evaporación de agua en canales de riego).
En cualquier caso, este tipo de problemas es uno de los más interesantes de la teoría de grafos y de la investigación operativa. Su aplicación es visible y de gran importancia para la resolución de problemas reales en la dirección de operaciones y logística.
problema del transbordo (coste mínimo)
Se puede considerar un grafo como una red de flujo. Donde los nodos proveedor producen o introducen en la red cierta cantidad de algún tipo de material, y los nodos cliente lo consumen. Cada arco, por tanto, puede considerarse como un conducto que tiene cierta capacidad de flujo (mínima y/o máxima) y un coste de transporte por unidad de material.
Dado un grafo dirigido <tex>G=(V,E)</tex> con capacidades <tex>c</tex> (mínima y/o máxima) no negativas y también con coste de transporte no negativo (expresado por unidad de flujo) para los arcos <tex>E</tex>.
Dado un conjunto de nodos <tex>X</tex> proveedores (con una capacidad <tex>b<0</tex> de suministro), y también un conjunto <tex>Y</tex> de nodos clientes (con una demanda <tex>b>0</tex>). En este caso particular, además se consideran nodos de transbordo (con valor de <tex>b=0</tex>), esto es nodos, que ni aportan ni consumen mercancías y donde éstas simplemente cambian de arco o hacen un transbordo.
Además, se exige la condición de continuidad en los nodos. Esto es, la suma de flujos entrantes a un nodo menos la suma de los salientes, debe ser mayor o igual a la capacidad <tex>b</tex> del nodo.
Por tanto, el problema de flujo máximo se enuncia como: ¿cuál es el flujo de transporte de cada arco con el cual se puede transportar el material desde los nodos proveedores a los nodos cliente, sin violar las restricciones de capacidad y continuidad y todo ello minimizando el coste total de transporte?.
La función objetivo queda expresada como:
<tex> \displaystyle{\min \sum_{i=1}^m\sum_{j=1}^n {c_{ij} x_{ij}}}</tex>
y está sujeto a las restricciones:
<tex> \displaystyle{\sum_{k=1}^m {x_{ki}} - \sum_{j=1}^m {x_{ij}} \quad \forall {j=1 \ldots m}} </tex>
<tex> \displaystyle{x_{ij} \geq 0, x_{ij} \in Z}</tex>
donde:
<tex> \displaystyle{b_i > 0 }</tex> demanda
<tex> \displaystyle{b_i < 0 }</tex> oferta
<tex> \displaystyle{b_i = 0 }</tex> transbordo
En el caso de Grafos, este problema se aborda a través del modelado y resolución mediante Programación Lineal. Igualmente, se pueden resolver problemas de: transporte de mercancías (logística de aprovisionamiento y distribución), flujo de gases y líquidos por tuberías, componentes o piezas en líneas de montaje, corriente en redes eléctricas, paquetes de información en redes de comunicaciones, tráfico ferroviario, sistema de regadíos, etc.
El problema de transbordo, se puede transformar en un problema clásico de flujo mínimo coste añadiendo un único nodo proveedor <tex>s</tex> y un único nodo de demanda <tex>t</tex> (ver Hitchcock-Koopmans, método Out-of-Kilter). Para que dicho problema sea factible, la suma del suministro total debe ser mayor o igual que el total de demanda (equilibrado).
problema del transporte (coste mínimo)
El problema del transporte es un problema de transbordo pero con un grafo dividido <tex>G=(S,T,E)</tex>, con todos los nodos suministradores en <tex>S</tex> y los de demanda en <tex>T</tex>. Además, todos los arcos van dirigidos de <tex>S</tex> a <tex>T</tex> y no existen nodos de transbordo.
El Problema de Asignación es un caso especial del problema de transporte, en el cual hay el mismo número de nodos suministradores que de demanda y los valores de nodos <tex>b= \pm 1</tex>.
Puede encontrar más información en:
- Hitchcock, F. L.,The distribution of a Product from Several Sources to Numerous Localities, J. Math. Phys., 20, no. 2 (April 1941), 224-30.
- Kuhn, H. W., The Hungarian Method for the Assignment Problem, Naval Research Logistics Quaterly, 2, nos. 1 and 2 (1955), 83-97.
- Ford, L. R. and Fulkerson, D. R. Flows in Networks. Princeton, NJ: Princeton University Press, 1962.
- Edmonds, J. and Karp, R. M. Theoretical Improvements in Algorithmic Efficiency for Network Flow Problems. J. ACM 19, 248-264, 1972.
- Zadeh. N, A Bad Network Problem for the Simplex Method and other Minimum Cost Flow Algorithms, Math. Prog., 5, no. 3 (December 1973), 255-66.
ejemplo de problema de transbordo
En primer lugar comenzaremos creando un conjunto de seis nodos con las siguientes etiquetas y valores:
ba 5 be 5 du 5 mu -500 nu -500 st -500
Seguidamente podremos crear los arcos, introduciendo sus valores de mínimo, máximo y coste:
Matriz de mínimo: N1\N2 ba be du mu nu st ba be 2 du 0 mu 2 0 2 0 2 nu 0 0 2 0 2 st 2 2 0 2 2 Matriz de máximo: N1\N2 ba be du mu nu st ba be 100 du 100 mu 100 100 100 100 100 nu 100 100 100 100 100 st 100 100 100 100 100 Matriz de coste: N1\N2 ba be du mu nu st ba be 10 du 10 mu 37 60 63 17 22 nu 43 44 44 17 19 st 27 63 41 22 19
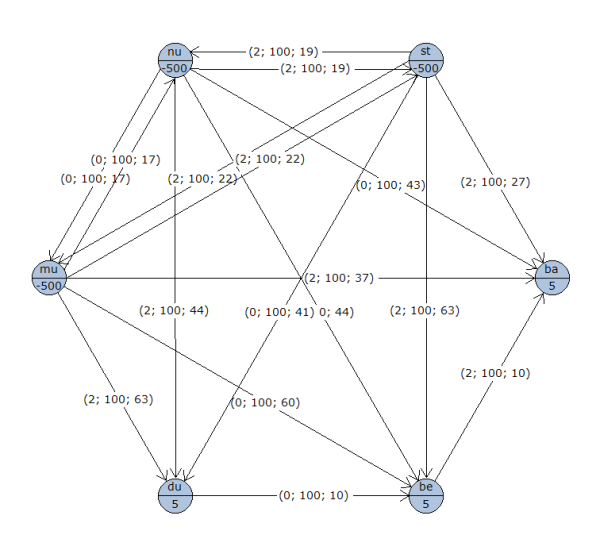
El grafo resultante quedará como muestra la siguiente imagen:
Al pulsar la correspondiente opción del menú, ocurrirá lo siguiente:
- Grafos interpretará los datos del problema y comprobará que todo es coherente, en caso negativo avisará al usuario
- Si todo es correcto, creará el sistema de ecuaciones a partir del modelo MILP anteriormente explicado
- Ejecutará el solver MILP, y comenzará el proceso de optimización. Esto requerirá mucho tiempo de cómputo si el problema es grande y compejo.
- Transcurrido el tiempo necesario, mostrará los resultados con la solución óptima encontrada o aviso de no factibilidad (en el caso de no poder satisfacer todas las restricciones impuestas en el problema).
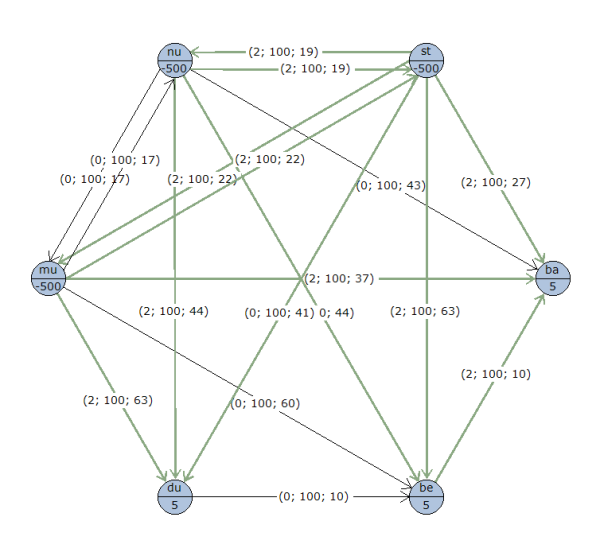
- Por último, interpretará la solución y dibujará los resultados en modo gráfico, tal y como muestra la siguiente imagen para este ejemplo.
- Además, Grafos mostrará en el cuadro de Resultados del Análisis del:

- Modelo en formato .lp
- Modelo en formato .mps
- Análisis de sensibilidad (de la función objetivo y de las restricciones)
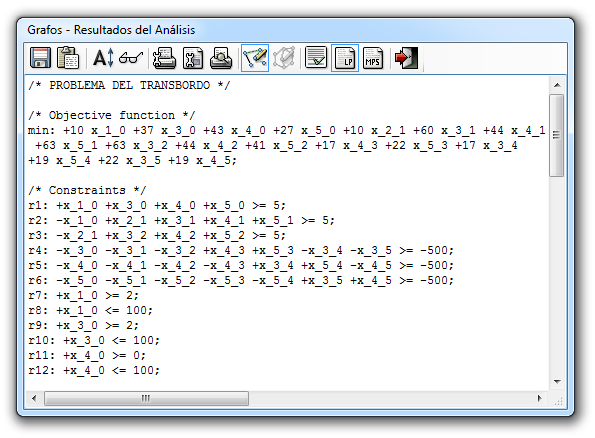
En este caso, la solución óptima encontrada tiene un valor de la función objetivo de 913 unidades, el resto de variables se muestran en el siguiente cuadro.
Valor de la función objetivo = 913 Valor actual de las variables: x_1_0:: be --> ba = 2 x_3_0:: mu --> ba = 2 x_4_0:: nu --> ba = 0 x_5_0:: st --> ba = 2 x_2_1:: du --> be = 0 x_3_1:: mu --> be = 0 x_4_1:: nu --> be = 5 x_5_1:: st --> be = 2 x_3_2:: mu --> du = 2 x_4_2:: nu --> du = 2 x_5_2:: st --> du = 1 x_4_3:: nu --> mu = 0 x_5_3:: st --> mu = 2 x_3_4:: mu --> nu = 0 x_5_4:: st --> nu = 2 x_3_5:: mu --> st = 2 x_4_5:: nu --> st = 2