algoritmo de Hierholzer
circuito euleriano
Carl Hierholzer (n. 2 de octubre, 1840 en Friburgo de Brisgovia - 13 de septiembre, 1871) fue un matemático alemán. Estudió matemáticas en la Universidad de Karlsruhe, y obtuvo su doctorado en la Universidad de Heidelberg en 1865. Su supervisor durante el doctorado fue Ludwig Otto Hesse (1811–1874). En 1870 Hierholzer escribió su habilitación sobre secciones canónicas, titulada Ueber Kegelschnitte im Raum, en Karlsruhe, donde posteriormente fue profesor.
Hierholzer demostró que un grafo tiene un ciclo euleriano si y sólo si es conexo y cada vértice tiene grado par. Este resultado había sido dado, sin demostración, por Leonhard Euler en 1736. Hierholzer aparentemente dio la demostración justo antes de su prematura muerte en 1871, a un colega que luego organizó el contenido para su publicación póstuma, la cual apareció en 1873, bajo el nombre Über die Möglichkeit, einen Linienzug ohne Wiederholung und ohne Unterbrechung zu umfahren.
Puede encontrar más información en:
algoritmo de Hierholzer (circuito euleriano)
A continuación se muestra el pseudocódigo del Algoritmo:
ListaArcosCircuito_K = vacío NodoUsado = false ArcoDisponible = true se toma NodoInicial NodoUsado(NodoInicial) = true Añadir NodoInicial a ListaNodosUsados TrazarCircuito (desde NodoInicial, ArcoDisponible, ListArcosCircuito_K) DO UNTIL que ListaNodosUsados = vacío Tomar último vértice u en ListaNodosUsados Borrar u de ListaNodosUsados ListArcosCircuito = vacío TrazarCircuito (desde NodoInicial, ArcoDisponible, ListArcosCircuito_C) Insertar ListArcosCircuito_C delante de posición arco en ListArcosCircuito_K LOOP
ejemplo de circuito euleriano
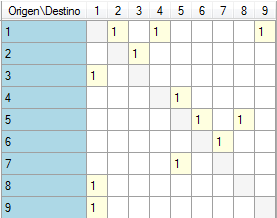
Para comprender mejor el funcionamiento del algoritmo de Hierholzer puede seguir este sencillo ejemplo. En primer lugar construya el siguiente grafo euleriano a partir de su matriz de distancias.
N1\N2 1 2 3 4 5 6 7 8 9 1 1 1 1 2 1 3 1 4 1 5 1 1 6 1 7 1 8 1 9 1
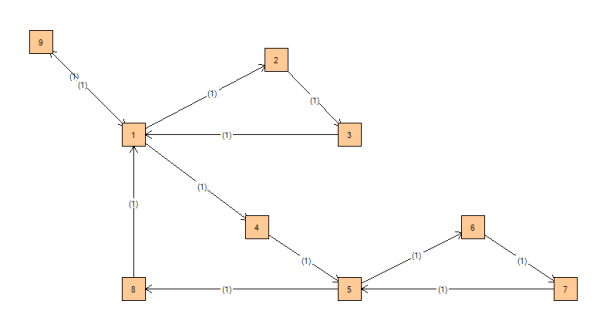
El resultado dibujado será más o menos como muestra la siguiente imagen.
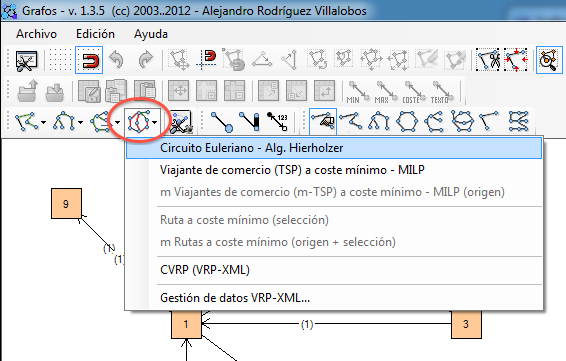
Seguidamente, pulse la opción de menú Circuito euleriano - Alg. Hierholzer, tal y como indica la siguiente imagen:
Rápidamente aparecerá la solución, marcando los arcos del circuito euleriano:
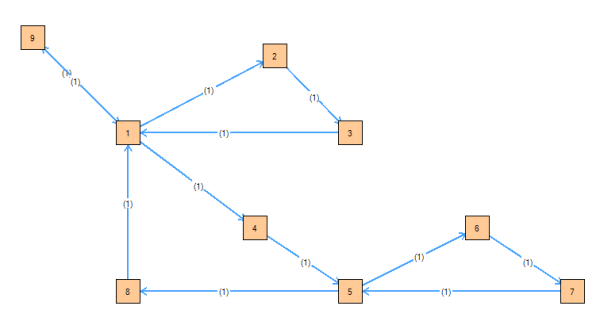
y la ventana con el texto de la solución:
Arcos del circuito euleriano:
* 1 ----(1)---> 2
* 2 ----(1)---> 3
* 3 ----(1)---> 1
* 1 ----(1)---> 4
* 4 ----(1)---> 5
* 5 ----(1)---> 6
* 6 ----(1)---> 7
* 7 ----(1)---> 5
* 5 ----(1)---> 8
* 8 ----(1)---> 1
* 1 ----(1)---> 9
* 9 ----(1)---> 1
Coste total = 12
Secuencia de nodos en el circuito:
1-2-3-1-4-5-6-7-5-8-1-9-1
Como este grafo es de grado par, el grafo es euleriano. En este caso, su grado máximo es 6, y su grado mínimo es 2.
En el caso de que el grafo no sea euleriano, Grafos le informará automáticamente y el algoritmo no se ejecutará. En ese caso, puede probar a cambiar las conexiones entre los vértices para intentar construir un circuito euleriano.