algoritmo de Floyd-Warshall

camino mínimo entre todos los pares de nodos

Robert W. Floyd nació el 8 de junio de 1936 en Nueva York, es profesor de la Stanford University (B.A. Chicago 1955 B.S. Chicago 1958), y en 1978 fue galardonado con el prestigioso premio A.M. Turing que otorga la ACM para reconocer las contribuciones de naturaleza técnica realizadas a la comunidad informática. El premio le fue concedido por tener una influencia clara en las metodologías para la creación de software eficiente y fiable, y por ayudar a fundar las siguientes áreas de la informática: teoría de análisis sintáctico, semántica de los leguajes de programación, verificación automática de programas, síntesis automática de programas y análisis de algoritmos.

Fue uno de los inventores del deterministic linear time selection algorithm. También introdujo mejoras en los algoritmos quicksort y quickselect.

algoritmo de Floyd-Warshall (todos los caminos mínimos)

El problema que intenta resolver este algoritmo es el de encontrar el camino más corto entre todos los pares de nodos o vértices de un grafo. Esto es semejante a construir una tabla con todas las distancias mínimas entre pares de ciudades de un mapa, indicando además la ruta a seguir para ir de la primera ciudad a la segunda. Este es uno de los problemas más interesantes que se pueden resolver con algoritmos de grafos.

Existen varias soluciones a este problema y los algoritmos a aplicar dependen también de la existencia de arcos con pesos o costes negativos en el grafo. En el caso de no existir pesos negativos, sería posible ejecutar V veces el algoritmo de Dijkstra para el cálculo del camino mínimo, donde V es el número de vértices o nodos del grafo. Esto conllevaría un tiempo de ejecución de O(V^3) (aunque se puede reducir). Si existen arcos con pesos negativos, se puede ejecutar también V veces el Algoritmo de Bellman-Ford, una vez para cada nodo del grafo. Para grafos densos (con muchas conexiones o arcos) esto conllevaría un tiempo de ejecución de O(V^4).

El algoritmo de Floyd-Warshall ('All-Pairs-Shortest-Path' - Todos los caminos mínimos) ideado por Floyd en 1962 basándose en un teorema de Warshall también de 1962, usa la metodología de Programación Dinámica para resolver el problema. Éste puede resolver el problema con pesos negativos y tiempos de ejecución iguales a O(V^33); sin embargo, para ciclos de peso negativo el algoritmo tiene problemas. A continuación se muestra el pseudocódigo del algoritmo: 

Floyd-Warshall (G)

Inicializar
    D = A ' matriz de distancias = matriz de arcos
 
    si i=j o Dij= infinito entonces Pi,j = nulo sino Pi,j=i 'matriz de caminos

for k = 1 to V
       for i = 1 to V 
            for j = 1 to V 
                   Di,j = min(Di,j , Di,k + Dk,j ) 
                        si min = Di,k + Dk,j entonces 
                            Pi,j = Pk,j  
fin

Este algoritmo se puede aplicar a multitud de problemas, incluyendo el diseño de circuitos, el diseño de rutas de transporte, aproximaciones al problema del viajante de comercio, o como base de otros algoritmos más complejos.

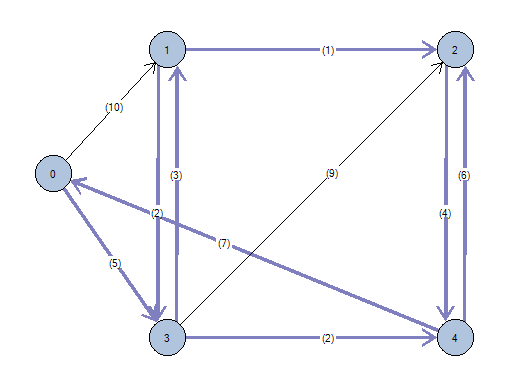
ejemplo de camino mínimo entre todos los pares de nodos

Para la ejecución de este algoritmo en Grafos no se requiere de la selección de ningún nodo origen o destino. Como su nombre indica, el algoritmo proporcionará todos los posibles caminos mínimos entre cada par de nodos origen y destino. En cierto modo es equivalente a ejecutar n × n veces el algoritmo de Dijkstra eligiendo a cada paso el nodo origen y destino i-j correspondiente.

Grafos subrayará todos los arcos que formen parte de algún camino mínimo. Los itinerarios o caminos entre pares de nodos aparecerán descritos en el texto del análisis. Es importante comprender el significado de la matriz de distancias mínimas y de la matriz de caminos.

ejemplo de todos los caminos mínimos 

Matriz de Distancias mínimas:

N1\N2	0	1	2	3	4	
0	0	8	9	5	7	
1	11	0	1	2	4	
2	11	19	0	16	4	
3	9	3	4	0	2	
4	7	15	6	12	0	

Matriz de Caminos:

N1\N2	0	1	2	3	4	
0	-	3	1	0	3	
1	4	-	1	1	3	
2	4	3	-	0	2	
3	4	3	1	-	3	
4	4	3	4	0	-	

Listado de Caminos:

0 --(0)--> 0 = 
0 --(8)--> 1 = 0, 3, 1
0 --(9)--> 2 = 0, 3, 1, 2
0 --(5)--> 3 = 0, 3
0 --(7)--> 4 = 0, 3, 4
1 --(11)--> 0 = 1, 3, 4, 0
1 --(0)--> 1 = 
1 --(1)--> 2 = 1, 2
1 --(2)--> 3 = 1, 3
1 --(4)--> 4 = 1, 3, 4
2 --(11)--> 0 = 2, 4, 0
2 --(19)--> 1 = 2, 4, 0, 3, 1
2 --(0)--> 2 = 
2 --(16)--> 3 = 2, 4, 0, 3
2 --(4)--> 4 = 2, 4
3 --(9)--> 0 = 3, 4, 0
3 --(3)--> 1 = 3, 1
3 --(4)--> 2 = 3, 1, 2
3 --(0)--> 3 = 
3 --(2)--> 4 = 3, 4
4 --(7)--> 0 = 4, 0
4 --(15)--> 1 = 4, 0, 3, 1
4 --(6)--> 2 = 4, 2
4 --(12)--> 3 = 4, 0, 3
4 --(0)--> 4 =