algoritmo de Dijkstra
camino mínimo/máximo, árbol mínimo/máximo, camino crítico
 Edsger Wybe Dijkstra nació en Rotterdam, (Holanda) en 1930. Sus padres eran ambos intelectuales y él recibió una excelente educación. Su padre era químico y su madre matemática. En 1942, cuando Dijkstra tenía 12 años, entró en Gymnasium Erasminium, una escuela para estudiantes especialmente brillantes, donde dio clases, fundamentalmente, de Griego, Latín, Francés, Alemán, Inglés, biología, matemáticas y química. En 1945, Dijkstra pensó estudiar Derecho y trabajar como representante de Holanda en las Naciones Unidas.
Edsger Wybe Dijkstra nació en Rotterdam, (Holanda) en 1930. Sus padres eran ambos intelectuales y él recibió una excelente educación. Su padre era químico y su madre matemática. En 1942, cuando Dijkstra tenía 12 años, entró en Gymnasium Erasminium, una escuela para estudiantes especialmente brillantes, donde dio clases, fundamentalmente, de Griego, Latín, Francés, Alemán, Inglés, biología, matemáticas y química. En 1945, Dijkstra pensó estudiar Derecho y trabajar como representante de Holanda en las Naciones Unidas.
Sin embargo, debido a su facilidad para la química, las matemáticas y la física, entró en la Universidad de Leiden, donde decidió estudiar física teórica. Durante el verano de 1951, asistió a un curso de verano sobre programación en la Universidad de Cambridge. A su vuelta empezó a trabajar en el Centro Matemático en Amsterdam, en marzo de 1952, donde se incrementó su creciente interés en la programación. Cuando terminó la carrera se dedicó a problemas relacionados con la programación. Pero uno de los problemas con que se encontró es que ser programador no estaba oficialmente reconocido como una profesión. De hecho, cuando solicitó una licencia de matrimonio en 1957, tuvo que señalar que su profesión era físico teórico.
Dijkstra continuó trabajando en el Centro Matemático hasta que aceptó un trabajo como desarrollador en Burroughs Corporation, en los Estados Unidos, a principio de la década de los 70. En 1972 ganó el Premio Turing ACM, y ,en 1974, el AFIPS Harry Good Memorial. Dijkstra se trasladó a Austin, Texas a principio de los 80. En 1984, se le ofreció un puesto en Ciencias de la Computación en la Universidad de Texas, donde permaneció desde entonces hasta que recientemente el 6 Agosto del 2002, Edsger W. Dijkstra, Professor Emeritus of Computer Sciences and Mathematics at The University of Texas en Austin, falleció en su hogar de Nuenen, (Netherlands). Es miembro honorario de la Academia Americana de Artes y Ciencias y de Real Academia Holandesa de Artes y Ciencias. Además es miembro distinguido de la Sociedad de Computación Británica. Finalmente es Doctor Honoris Causa en Ciencias por la Queen's University Belfast.
algoritmo de Dijkstra (ruta más corta - árbol mínimo - camino mínimo)
En 1956, Dijkstra anunció su algoritmo de caminos mínimos, después de haber estado trabajando con el ARMAC, el ordenador que el Centro Matemático poseía.
Más tarde propuso el algoritmo del árbol generador minimal. A principios de la década de los 60, Dijkstra aplicó la idea de la exclusión mutua a las comunicaciones entre una computadora y su teclado. Su solución de exclusión mutua ha sido usada por muchos procesadores modernos y tarjetas de memoria desde 1964, cuando IBM la utilizó por primera vez en la arquitectura del IBM 360. El siguiente problema del que se ocupó Dijkstra fue el de los filósofos comensales. En este problema, cinco filósofos están sentados en una mesa circular con un plato de arroz delante y un palillo a cada lado, de manera que hay cinco palillos en total. El problema trata sobre el uso de recursos comunes sin que los procesos (los filósofos) lleguen a una situación de bloqueo mutuo, inanición y que los recursos sean usados de la manera más eficiente por todos los procesos. También ayudó a fomentar la disciplina en la programación: “GOTO se puede considerar dañino. Cuanto más sentencias GOTO haya en un programa, más difícil es entender el código fuente”.
Una red de comunicaciones involucra un conjunto de nodos conectadas mediante arcos, que transfiere vehículos desde determinados nodos origen a otros nodos destino. La forma más común para seleccionar la trayectoria (o ruta) de dichos vehículos, se basa en la formulación de la ruta más corta. En particular a cada arco se le asigna un escalar positivo el cual se puede ver como su longitud.
Un algoritmo de trayectoria más corta, rutea cada vehículo a lo largo de la trayectoria de longitud mínima (ruta más corta) entre los nodos origen y destino. Hay varias formas posibles de seleccionar la longitud de los enlaces. La forma más simple es que cada enlace tenga una longitud unitaria, en cuyo caso, la trayectoria más corta es simplemente una trayectoria con el menor número de enlaces. De una manera más general, la longitud de un enlace puede depender de su capacidad de transmisión y su carga de tráfico.
La solución es encontrar la trayectoria más corta. Esperando que dicha trayectoria contenga pocos enlaces no congestionados; de esta forma los enlaces menos congestionados son candidatos a pertenecer a la ruta. Hay algoritmos de ruteo especializados que también pueden permitir que la longitud de cada enlace cambie en el tiempo, dependiendo del nivel de tráfico de cada enlace. De esta forma un algoritmo de ruteo se debe adaptar a sobrecargas temporales y rutear paquetes alrededor de nodos congestionados. Dentro de este contexto, el algoritmo de ruta más corta para ruteo opera contínuamente, determinando la trayectoria más corta con longitudes que varían en el tiempo.1)
El problema de la ruta más corta se puede resolver utilizando programación lineal sin embargo, debido a que el método simplex es de complejidad exponencial, se prefiere utilizar algoritmos que aprovechen la estructura en red que se tiene para estos problemas. Para ello, el algoritmo mantiene un conjunto S de nodos cuyos pesos finales de camino mínimo desde el nodo origen ya han sido determinados. A continuación se muestra el pseudocódigo del Algoritmo:
Dijkstra (G,s)
Inicializar
for cada v perteneciente a V[G]
do d[v] = infinito
p[v] = nulo
d[s] = 0
S = vacio
Q = V[G]
mientras Q no vacio
do u = nodo v con min d[v]
S = S unión u 'se añade al conjunto de nodos finalizados
for cada v perteneciente Adyacente u
Relajación
if d[v] > d[u] + w(u,v) then
d[v] = d[u] + w(u,v)
p(v) = u
algoritmo de Dijkstra (ruta más larga - árbol máximo - camino crítico)
El camino crítico estará formado por tareas críticas (nodos) cuya duración (coste del arco sucesor) determina la duración total de un proyecto. Si una tarea crítica se retrasa o su duración cambia durante la realización del proyecto, afectaría directamente a la duración total del proyecto y a su fecha de finalización.
Encontrar el camino crítico de la planificación de un proyecto es lo mismo que encontrar el camino más largo desde el nodo inicial (tarea inicial) al nodo final (última tarea); esto es, la mínima cantidad de tiempo necesaria para finalizar un proyecto.
El algoritmo de Dijkstra aunque fue diseñado para encontrar la ruta más corta se puede transformar fácilmente para encontrar la ruta más larga (camino crítico), cambiando simplemente su función objetivo. Del mismo modo, se encuentra el árbol máximo desde un nodo origen.
Puede encontrar más información en:
- Video sobre Dijkstra subtitulado en inglés (MPG 300 Mb) (University of Texas - VPRO TV)
- Dijkstra, E., A note on two problems in connexion with graphs, Numerische Mathematik 1, 269-271, 1959.
ejemplo de camino mínimo
Para comprender mejor el funcionamiento del algoritmo puede seguir este sencillo ejemplo. En primer lugar construya el siguiente grafo a partir de su matriz de distancias.
N1\N2 0 1 2 3 4 0 10 5 1 1 2 2 4 3 3 9 2 4 7 6
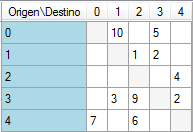
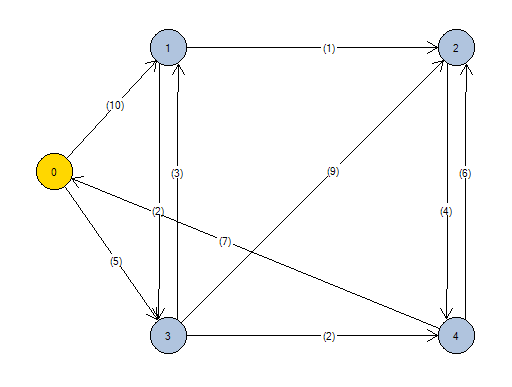
El resultado dibujado será como muestra la siguiente imagen.
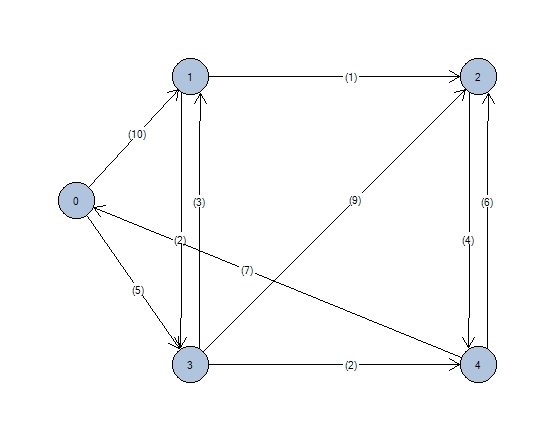
Seguidamente elija el nodo 0 como origen, y el nodo 4 como destino. El algoritmo de Dijkstra (camino mínimo) se activará en el menú y podrá ser utilizado.
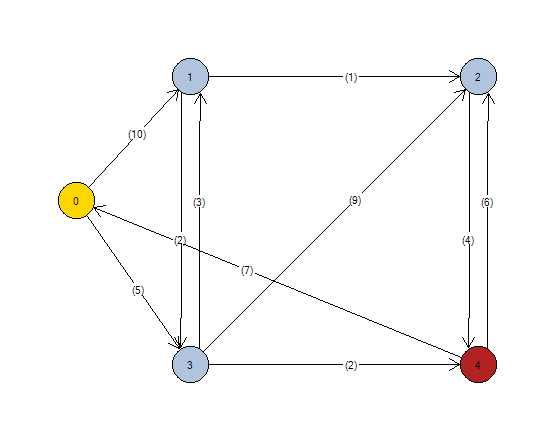
Tras el cálculo, se mostrará la solución tal y como muestra la siguiente imagen.
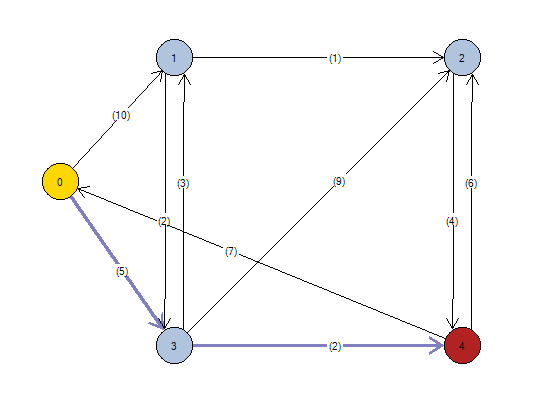
Los arcos subrayados forman parte del camino mínimo que une siguiendo la dirección de los arcos, el nodo origen 0 elegido hasta llegar al nodo destino 4. De todas las posibles conexiones existentes entre el nodo origen y el nodo destino, el algoritmo de Dijkstra proporciona el camino mínimo óptimo, es decir, el de menor distancia o coste total de todos los posibles; que en este caso tiene un coste total de 7 unidades.
Arcos calculados desde el nodo origen (0) hasta el nodo destino (4): * 0 ----(5)---> 3 * 3 ----(2)---> 4 Coste total = 7 Matriz de Arcos con coste mínimo: N1\N2 0 1 2 3 4 0 0 0 0 1 0 1 0 0 0 0 0 2 0 0 0 0 0 3 0 0 0 0 1 4 0 0 0 0 0
En el caso de que existan varias soluciones mínimas, empate en el óptimo, el algoritmo de Dijkstra sólo mostrará una de ellas.
ejemplo de árbol mínimo
Con el mismo grafo anterior, seguidamente se calculará el árbol mínimo que une el nodo origen 0 con el resto de nodos. Para ello, se selecciona el nodo origen y se ejecuta el algoritmo de Dijkstra para el árbol mínimo.
El resultado óptimo con un coste total de 11 unidades es el siguiente:
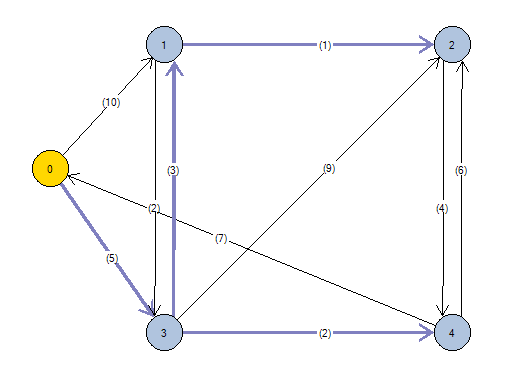
Arcos calculados desde el nodo origen (0):
0 ----(5)---> 3
1 ----(1)---> 2
3 ----(3)---> 1
3 ----(2)---> 4
Matriz de Arcos con coste mínimo:
N1\N2 0 1 2 3 4
0 0 0 0 1 0
1 0 0 1 0 0
2 0 0 0 0 0
3 0 1 0 0 1
4 0 0 0 0 0
El resto de arcos si bien podría conectar el conjunto de nodos, añadiría costes adicionales sobre el óptimo. Cabe recordar, que la solución dependerá de la estructura y costes del grafo, así como de los nodos seleccionados.
De manera similar a estos ejemplos, pero con efecto contrario, se calcularía el camino máximo y el árbol de coste máximo.
ejemplo de camino máximo
El cálculo del camino máximo se realiza del mismo modo, pero arrojará los resultados contrarios. La siguiente imagen muestra la solución para este caso con un coste máximo de 25 unidades.
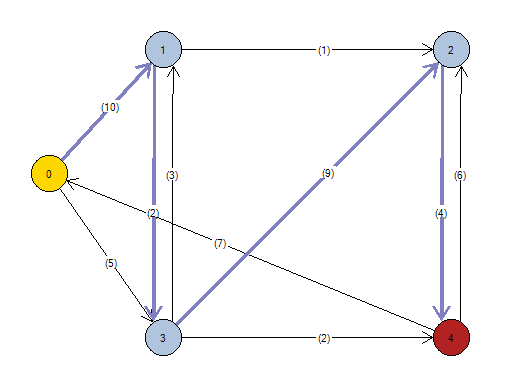
Arcos calculados desde el nodo origen (0) hasta el nodo destino (4): * 0 ----(10)---> 1 * 1 ----(2)---> 3 * 2 ----(4)---> 4 * 3 ----(9)---> 2 Coste total = 25 Matriz de Arcos con coste máximo: N1\N2 0 1 2 3 4 0 0 1 0 0 0 1 0 0 0 1 0 2 0 0 0 0 1 3 0 0 1 0 0 4 0 0 0 0 0